Linear neural network to creat $f(x)= W^{\top}x$

Goal:

In this post we are going to go through the very first step that help us to suppress algebraic notations for representing the function calculating by a fully connected neural network. Following this step helps you to master shorthand notations to express operations happening in the neural network.

A linear function in the form of $f(x)= W^{\top}x$

In the previous post we discussed how to find the Jacobian matrix of $f(x)= Ax$ where $A \in \mathbb{R}^{m \times n}$ and $x = [x_1, x_2, \cdots, x_n]^{\top}$. Also, I showed how to represent $f(x)$ in terms of rows of $A$. However, here, we are dealing with $W^{\top}$ in place of $A$ where $W \in \mathbb{R}^{n \times m}$  which requires us to do some work. In order to show how we can build this function using a linear neural network. Suppose $y= f(x)$. Therefore, each coordinate of $f(x)$ equals to each coordinate of a $y$. That is

$$
\begin{align}
y &=
\begin{bmatrix}
y_1\\
y_2\\
\vdots\\
y_n
\end{bmatrix} =
f(x)=W^{\top}x\\
&\stackrel{(1)}{=}
\begin{bmatrix}
W_{\bullet1} & W_{\bullet2} & \cdots & W_{\bullet m}
\end{bmatrix}^{\top}x\\
&\stackrel{(2)}{=}
\begin{bmatrix}
W_{\bullet 1}\\
W_{\bullet 2}\\\\
\vdots\\
W_{\bullet m}\\
\end{bmatrix}x
\stackrel{(3)}{=}
\begin{bmatrix}
W_{\bullet 1}x\\
W_{\bullet 2}x\\\\
\vdots\\
W_{\bullet m}x\\
\end{bmatrix}\\
&\stackrel{(4)}{=}
\begin{bmatrix}
w_{11}x_1 + w_{21}x_2 + \cdots + w_{n1}x_n\\
w_{12}x_1 + w_{22}x_2 + \cdots + w_{n2}x_n\\
\vdots\\
w_{1m}x_1 + w_{2m}x_2 + \cdots + w_{nm}x_n\\
\end{bmatrix}
\end{align}
$$

where $W_{i\bullet}$ is the $i$-th row of $W$ and $W_{\bullet j}$ is the $j$-th column of $W$. Also,

• (1) is the representation of $W$ columnwise with $m$ columns($W \in \mathbb{R}^{n \times m}$)
• (2) is the transpose of $w$ so every column becomes a row
• (3) and (4) are because of matrix multiplication rule

I had promissed to represent $f(x)= W^{\top}x$ using neural network. To that end, look at the following simple neural network where we have only input and output layers. Input layer has $2$ elements and output layer has $3$ leyers. Each input gets multiplied by its corresponding weight and adds to the other product in order to build each element of $y$.

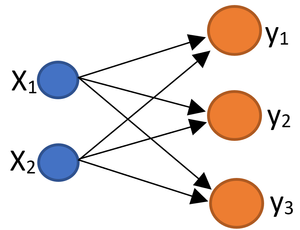
If I annotate every arrow using a weight $w$ whose first index is associated with input and second one with the output we have the following network.

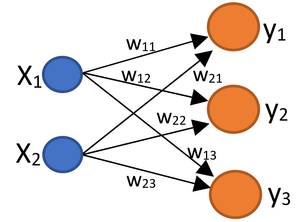
 If you carefully look, we can write each element of $y$ using linear combination of $x$'s element and $w$'s as the following

$$
\begin{align}
y &=
\begin{bmatrix}
y_1\\
y_2\\
y_3\\
\end{bmatrix} =
\begin{bmatrix}
W_{11}x_1 + W_{21}x_2 \\
W_{12}x_1 + W_{22}x_2 n\\
W_{13}x_1 + W_{23}x_2 \\
\end{bmatrix}\\
&=
\begin{bmatrix}
W_{11} & W_{21}\\
W_{12} & W_{22}\\
W_{13} & W_{23} \\
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}\\
&=
\begin{bmatrix}
W_{11} & W_{12} & W_{13}\\
W_{21} & W_{22} & W_{23}\\
\end{bmatrix}^{\top}
\begin{bmatrix}
x_1\\
x_2\\
\end{bmatrix}
=W^{\top}x = f(x)
\end{align}
$$

Hence, from now on, I will assign $W$ between each two layers because we can think of them as input($x$) and output($y$) where output formula is $y = W^{\top}x$.

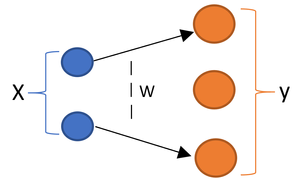
In the next post I will add another element to our function which is called biass and because of that our function would be $W^{\top}x + b$.